|
|||
Моделирование фигур Лиссажу |
|||
|
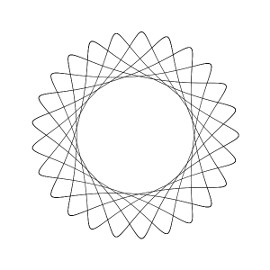
В сегодняшней статье мы обсудим такое понятие, как фигуры Лиссажу. Данный материал является хорошим дополнением к теме “Колебания и волны”, которая изучается в 9 классе школы. Рассмотрим материальную точку, находящуюся на плоскости X-Y. Для начала зафиксируем коррдинату X, а координату Y будем изменять по синусоидальному закону. Тогда точка будет совершать вертикальные колебания – такие же, как грузик на пружине. Если, наоборот, зафиксировать Y и изменять X, то это будут горизонтальные колебания. Если же позволить точке одновременно колебаться по X и Y, то получится некоторая траектория. Ее называют фигурой Лиссажу по имени ученого, который впервые это изучал. Допустим, точка успевает совершить одно колебание по горизонтали и одно колебание по вертикали. В этом случае фигура Лиссажу будет прямая линия, эллипс или окружность (в зависимости от начальных условий).
Если за один период горизонтальных колебаний точка совершит два вертикальных колебания, то фигура будет выглядеть как седло.
Более подробное теоретическое описание фигур можно найти в Википедии. Мы же в данной работе составили javascript-программу, которая отрисовывает фигуры по заданным коэффициентам: https://static.livescience.ru/lissazhu/lissazhu.html Кроме того, в нее добавлен параметр “сдвиг фазы”. При его активации каждый следующий кадр получает чуть больший фазовый сдвиг, так что фигура начинает красиво вращаться по горизонтали или вертикали. В реальной практике фигуры Лиссажу смотрят на экране осциллографа, подавая сигналы на входы “X” и “Y”. Если один из сигналов имеет известную частоту, то по внешнему виду фигуры можно понять, какую частоту имеет второй сигнал. Например, добившись на экране эллипса, мы сможем утверждать, что частоты обоих сигналов в точности равны.
|
Рассказать друзьям
| © | права на опубликованные материалы принадлежат их авторам |
Другие статьи этого раздела
Комментарии ( 1 )
-
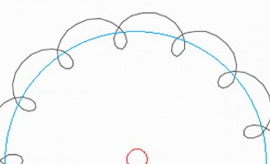
Еще интересен вариант, когда колебания являются затухающими. При этом получаются разные своеобразные поверхности: https://static.livescience.ru/lissazhu/lissazhu_zatuh.htmlAdministrator 17 декабря 2018, 18:07
Ваш комментарий